Persamaan Kuadrat

Persamaan kuadrat adalah suatu persamaan polinomial berorde dua. Bentuk umum dari persamaan kuadrat adalah

dengan

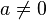
Huruf-huruf a, b dan c disebut sebagai koefisien: koefisien kuadrat a adalah koefisien dari x², koefisien linier b adalah koefisien dari x, dan c adalah koefisien konstan atau disebut juga suku bebas.

RUMUS-RUMUS DALAM PERSAMAAN KUADRAT

Rumus kuadratis dikenal pula dengan nama 'rumus abc karena digunakan untuk menghitung akar-akar persamaan kuadrat yang tergantung dari nilai-nilai a, b dan c suatu persamaan kuadrat. Rumus yang dimaksud memiliki bentuk

Rumus ini digunakan untuk mencari akar-akar persamaan kuadrat apabila dinyatakan bahwa

.

Dari rumus tersebut akan diperoleh akar-akar persamaan, sehingga persamaan semula dalam bentuk

dapat dituliskan menjadi

.

Dari persamaan terakhir ini dapat pula dituliskan dua hubungan yang telah umum dikenal, yaitu

dan

.

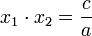DISKRIMINAN

Dalam rumus kuadrat di atas, terdapat istilah yang berada dalam tanda akar:

Diskriminan tersebut biasanya digunakan untuk mengetahui nilai dari akar-akar persamaan yang akan dicari. Sebagai contoh :

• Apabila nilai diskriminannya lebih dari nol (0) [D>0]  maka persamaan kuadrat tersebut mempunyai jenis akar yang riil dan berbeda.
• Apabila D=0 maka persamaan kuadrat tersebut mempunyai jenis akar yang sama atau kembar.
• Apabila D<0 maka persamaan kuadrat tersebut tidak mempunyai akar-akar yang riil/